Rysunek techniczny na G-code

Witam.
Stanąłem przed problemem jak za pomocą uniwersalnych G-codów (G0,G1,G2,G3) narysować taki rysunek z książki sinumerinka:


Właściwie to nie wiem jak obliczyć położenie brakującego promienia okręgu zaznaczonego na czerwono. Pierwszy punkt obliczyłem dzięki wzorom trygonometrycznym.

Proszę o pomoc i pozdrawiam.

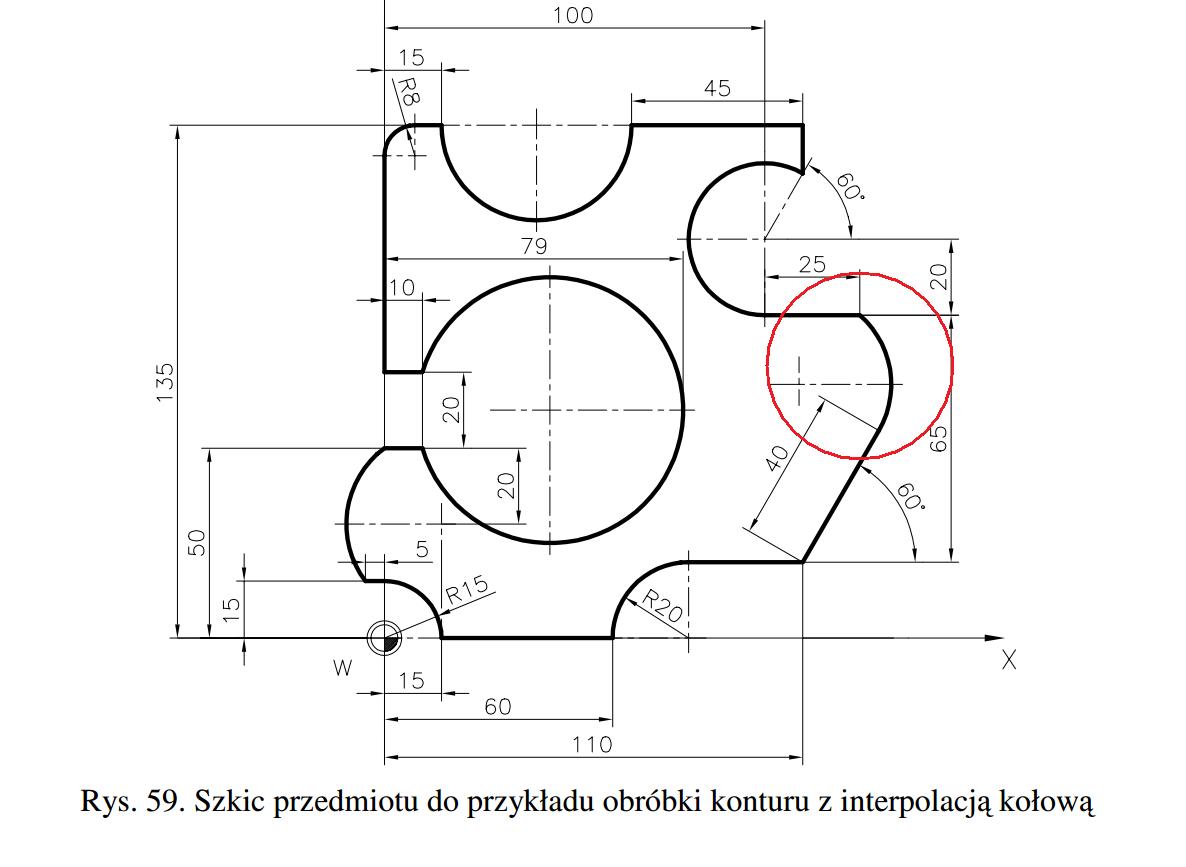
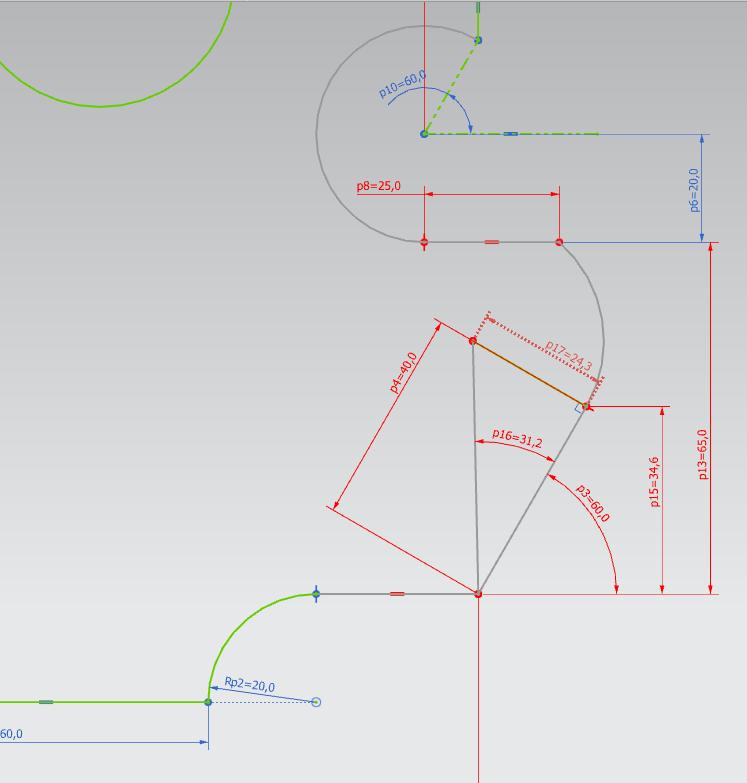
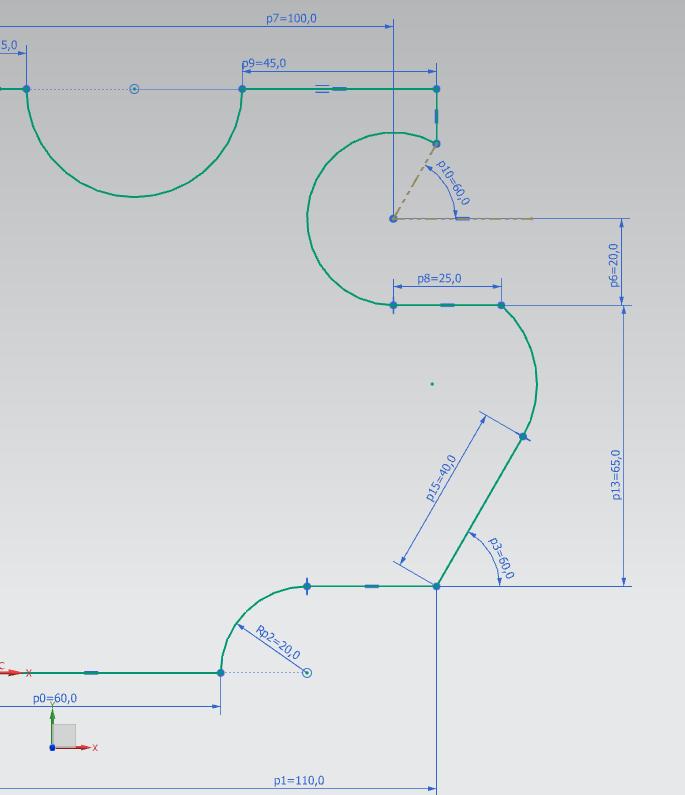
Jeden z punktów da się policzyć z funkcji trygonometrycznych. Jako punkt bazowy możemy potraktować sobie punkt, od którego wychodzi prosta pod kątem 40 stopni. Punkt początkowy prostej jest podany. Od zaznaczonego punktu bazowego w osi X = 110, w Y = 20 (biorąc pod uwagę że wychodzi od R20, a styczna do niego leci prostopadle do osi X).
Czyli od tego punktu obliczając Sin(60) i mnożąc przez długość przeciwprostokątnej, czyli 40, uzyskujemy wynik 34,641. I do wartości początkowej musimy dodać uzyskany wynik. Sin zawsze odpowiada osi Y, czyli współrzędne końca promienia w Y = 54.641. Z X zróbmy tak samo, tylko obliczając Cos, czyli Cos(60)*40 = 20, czyli X = 110+20 = 130.

Drugi punkt masz podany w osi X = 100+25, w Y = 20+65.

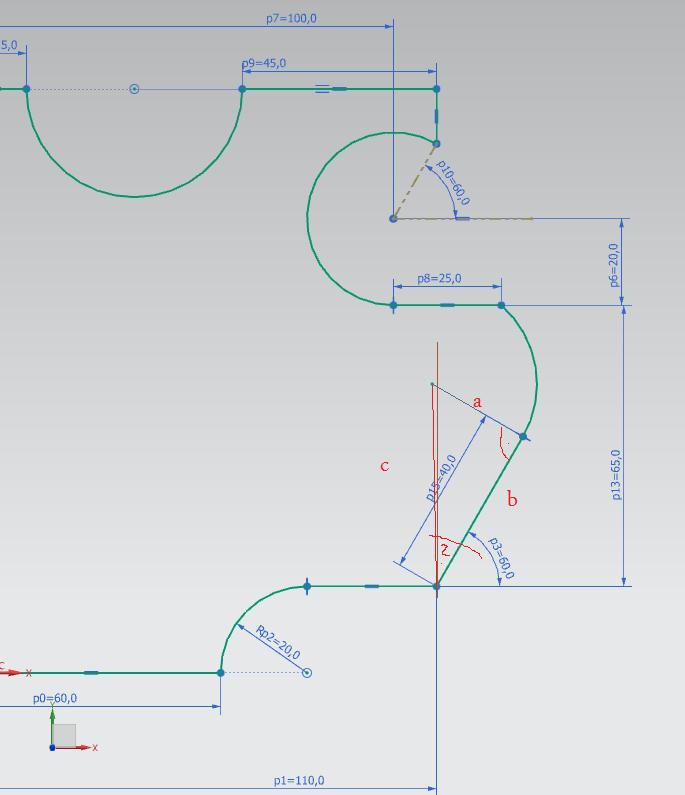
Środek okręgu możemy również wyliczyć z funkcji trygonometrycznych. Styczna do kręgu pada zawsze pod kątem 90 stopni do środka okręgu. Czyli jeśli prosta padająca pod kątem 60 stopni ma długość 40, i tworzy z prostą od jej punktu końcowego do środka okręgu kąt prosty, więc korzystając z Tan(30)*40 obliczymy długość drugiej przyprostokątnej. Następnie z Twierdzenia Pitagorasa obliczamy przeciwprostokątną = 46.188. Z powyższego wynika, że środek okręgu leży w punktach X = 110, Y = 66.188.
Można to również wyliczyć w inny sposób. Sin(150)*23.094 (długość przyprostokątnej z równania Tan(30)*40 jest teraz przeciwprostokątną), czyli środek okręgu od współrzędnych 54.641 jest oddalony o 11.547, Y = 54.641 + 11.547 = 66.188.
W X natomiast Cos(150)*23.094 = -20. Czyli X = 110.

Pozdrawiam

Właśnie te punkty sobie wyliczyłem i stoje na promieniu. Z tego co zapamiętałem funkcje G1 w sinumeriku dało sie opisać jakoś tak " G16 G1 X40 Y60" gdzie oczywiście x jest promieniem a y kątem. Podobnie dało się jakoś prosto przejść z prostej do okręgu znając tylko drugi jego punkt. Jednak było to 3 lata temu i zapomniałem jak to się robiło. Ogólnie to nie przypominam sobie żeby były takie problemy pisząc z "ręki".

Znając współrzędne środka okręgu problem masz rozwiązany.
(kierunek obrubki: współbierznie)

Narysowałem sobie to w NX i wychodzi na to że środek okręgu nie tworzy z wymiarem "25" linii prostej(dobrze to widać na zrzucie) Czyli kąt wynosi nie 30st a 31.23st długość promienia zmienia się znacząco. Nadal się zastanawiam jak to prawidłowo obliczyć.

Do "PiRo_man" niestety nie mogę określić środka okręgu o to właśnie chodzi.

A skąd wzięła Ci się wartość p17 = 24,3?

Szkic w NX jest zwymiarowany tak jak na rysunku technicznym czyli tak:


Jak widać wymiary wystarczyły do z wymiarowania. Czyli rysunek był dobry nic nie brakuje i nic nie jest za dużo. Teoretycznie da się to zrobić bez pomocy komputera


Te wymiary na czerwono we wcześniejszym zdjęciu oznaczają przewymiarowanie rysunku zrobiłem to celowo tylko po to żeby pokazać jakie są tam realne wartości.
Pozdrawiam i główkuje dalej.

nasiono pisze:kąt wynosi nie 30st a 31.23st

Tworzysz nową matematykę albo nie jestem na bieżąco. Od kiedy suma kątów w trójkącie może być większa od 180..?

BTW przeczytaj sobie jeszcze raz mojego pierwszego posta. Nie tyle że rozwiązałem Twój problem, to jeszcze udowodniłem że jest ono prawidłowe, i po kolei wytłumaczyłem wszystko co, jak i dlaczego.
Jeśli tego nie widzisz, to życzę powodzenia i główkuj dalej.

Również pozdrawiam

Problem w tym że linia zaznaczona na czerwono wcale nie jest prostopadła do osi X. Twoje obliczenia są prawidłowe ale dla warunku że prosta "c" jest prostopadła do X wtedy rzeczywiście między nią a prostą "b" byłby kąt 30 st. Niestety tak nie jest co widać dobrze w CADzie.
Pozdrawiam.

PiRo_man pisze:Znając współrzędne środka okręgu problem masz rozwiązany.
(kierunek obrubki: współbierznie)

Kod: Zaznacz cały

(...) 
G01 X125. Y85. F100
G2 X130. Y54.641 I-15. J-18.812
G1 X110. Y20.
(...)

.... to jaki R będzie tego okręgu w/g Twoich obliczeń , gdyż ja w/g tych danych nie mogę wpisać okręgu.

http://fotoo.pl/show.php?img=585099_bez ... u.jpg.html

Program w symulacji też nie przeszedł;

http://fotoo.pl/show.php?img=585117_ww.bmp.html



Mariusz.