moduł koła stożkowego ,kto wykona zębatke
-
tom102
Autor tematu - Czytelnik forum poziom 2 (min. 20)

- Posty w temacie: 8
- Posty: 23
- Rejestracja: 06 lip 2014, 15:25
- Lokalizacja: wąsosz
moduł koła stożkowego ,kto wykona zębatke
Witam
Jak można obliczyć moduł koła stożkowego o zębach prostych?
Przeszukałem już wiele stron na ten temat i niestety nie znalazłem odpowiedzi.
Jeżeli ktoś zna odpowiedz to z góry dziękuje.
Jak można obliczyć moduł koła stożkowego o zębach prostych?
Przeszukałem już wiele stron na ten temat i niestety nie znalazłem odpowiedzi.
Jeżeli ktoś zna odpowiedz to z góry dziękuje.
Ostatnio zmieniony 18 lut 2015, 19:09 przez tom102, łącznie zmieniany 1 raz.
Tagi:
Re: moduł koła stożkowego
Części maszyn - Andrzej Rutkowskitom102 pisze: Jak można obliczyć moduł koła stożkowego o zębach prostych?
Przeszukałem już wiele stron na ten temat i niestety nie znalazłem odpowiedzi.
lub każdy inny podręcznik traktujący o kołach zębatych
-
RomanJ4
- Lider FORUM (min. 2000)

- Posty w temacie: 12
- Posty: 11916
- Rejestracja: 17 mar 2009, 08:55
- Lokalizacja: Skępe
Jak każde inne koło zębate. Dzielisz obwód zewnętrzny na ilość zębów+2, i (w razie niedokładności związanej z pomiarem) bierzesz najbliższy znormalizowany. Ilość zębów z o danym module m(p) koła zębatego jest ściśle powiązana ze średnicą tego koła da,

wynikającą z przekształcenia wzoru:
m = da : z+2
gdzie:
m = moduł zębów koła
da = średnica zewnętrzna koła(wieńca)
z = ilość zębów
W zasadzie dla koła stożkowego (do przekładni o kącie 90°) wzór wyjsciowy na moduł m wygląda tak
Dp = z • mte
gdzie:
Dp - średnica podziałowa zewnętrzna stożka podziałowego
z - rzeczywista ilość zębów w kole
mte - czołowy moduł zewnętrzny
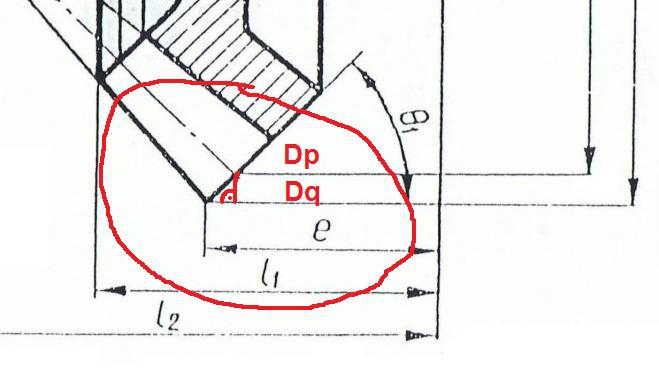
ale ten sam wzór na obliczenie m jak dla koła prostego(powyżej) możemy w praktyce bez wielkiego błędu zastosować do koła stożkowego, z tym że nasze da = Dq(na rysunku poniżej)

czyli: m = Dq : z+2

wynikającą z przekształcenia wzoru:
m = da : z+2
gdzie:
m = moduł zębów koła
da = średnica zewnętrzna koła(wieńca)
z = ilość zębów
W zasadzie dla koła stożkowego (do przekładni o kącie 90°) wzór wyjsciowy na moduł m wygląda tak
Dp = z • mte
gdzie:
Dp - średnica podziałowa zewnętrzna stożka podziałowego
z - rzeczywista ilość zębów w kole
mte - czołowy moduł zewnętrzny
ale ten sam wzór na obliczenie m jak dla koła prostego(powyżej) możemy w praktyce bez wielkiego błędu zastosować do koła stożkowego, z tym że nasze da = Dq(na rysunku poniżej)

czyli: m = Dq : z+2
pozdrawiam,
Roman
Roman
-
Grzegorz53
- Specjalista poziom 3 (min. 600)

- Posty w temacie: 1
- Posty: 602
- Rejestracja: 30 gru 2009, 23:21
- Lokalizacja: W-wa
-
tom102
Autor tematu - Czytelnik forum poziom 2 (min. 20)

- Posty w temacie: 8
- Posty: 23
- Rejestracja: 06 lip 2014, 15:25
- Lokalizacja: wąsosz
Witam
dzięki wszystkim za pomoc, zmierzyłem i policzyłem, błąd jest spory ,ale wydaje mi się że, będzie to moduł 3,5.
Problem jest teraz inny, jest ktoś na tym forum kto podejmie się wykonania takiej zębatki jak na zdjęciach.
Mogę ja przesłac jako wzór.
Zębatka współpracuje z większą 50z, przełożenie 1/2




dzięki wszystkim za pomoc, zmierzyłem i policzyłem, błąd jest spory ,ale wydaje mi się że, będzie to moduł 3,5.
Problem jest teraz inny, jest ktoś na tym forum kto podejmie się wykonania takiej zębatki jak na zdjęciach.
Mogę ja przesłac jako wzór.
Zębatka współpracuje z większą 50z, przełożenie 1/2




-
Cezary2528
- Stały bywalec (min. 70)

- Posty w temacie: 1
- Posty: 73
- Rejestracja: 01 sty 2012, 01:26
- Lokalizacja: Mrągowo
-
RomanJ4
- Lider FORUM (min. 2000)

- Posty w temacie: 12
- Posty: 11916
- Rejestracja: 17 mar 2009, 08:55
- Lokalizacja: Skępe
I będzie. Powinienem dopisać że może wyjść spory bo tak naprawdę we wzorze m = Dq : z+2 nie powinno być "2", tylko miedzy ~"1,5" a "2"(co trzeba by dokładnie wyliczyć) bo wysokość głowy zęba(miedzy Dp a Dq) jest funkcją trójkąta prostokątnego (przyprostokątną) ponieważ zarys zęba jest pochylony pod kątem 45° do osi kołatom102 pisze:zmierzyłem i policzyłem, błąd jest spory
pozdrawiam,
Roman
Roman
-
tom102
Autor tematu - Czytelnik forum poziom 2 (min. 20)

- Posty w temacie: 8
- Posty: 23
- Rejestracja: 06 lip 2014, 15:25
- Lokalizacja: wąsosz
Według mnie nie sprawia wrażenia płaskiej, możne zdjęcia trochę ja odchudzają jeszcze bardziej niż brakujące 13 zębów.Cezary2528 pisze:Dziwna ta zębatka, jakaś taka mało płaska
http://pl.wikipedia.org/wiki/Z%C4%99batka
Jest to zębatka od posuwu wzdłużnego suportu tokarki na wałku (zresztą od poprzecznego jest taka sama)
Jak będę przy maszynie to porobię zdjęcia całości.
Mam jeszcze jedno pytanie, na zębatce wybity jest numer 35. Co to oznacza?. Na początku myślałem, że chodzi właśnie o moduł 3,5 ale ten sam numer jest tez na innych częściach.
Znacie może kogoś kto by się podjął dorobienia takiej zębatki.
-
Areo84
- Specjalista poziom 3 (min. 600)

- Posty w temacie: 8
- Posty: 996
- Rejestracja: 26 gru 2009, 09:33
- Lokalizacja: ...
Jeśli przez błąd rozumiecie różnicę między modułem wyliczonym ze wzoru, który podał Roman (m = Dq : z+2 ), a najbliższym znormalizowanym modułem ta zwykle nie wychodzi on jakiś duży i raczej nie pwoinien znacząco odbiegać od najbliższego znormalizowanego.RomanJ4 pisze:I będzie. Powinienem dopisać że może wyjść spory bo tak naprawdę we wzorze m = Dq : z+2 nie powinno być "2", tylko miedzy ~"1,5" a "2"(co trzeba by dokładnie wyliczyć) bo wysokość głowy zęba(miedzy Dp a Dq) jest funkcją trójkąta prostokątnego (przyprostokątną) ponieważ zarys zęba jest pochylony pod kątem 45° do osi kołatom102 pisze:zmierzyłem i policzyłem, błąd jest spory
Przykładowo weźmy jakieś dowolne koło stożkowe , niech będą te z oferty EBMiA i policzmy moduł biorąc średnicę da według ich rysunku . Czyli m=da:z+2
www.ebmia.pl/kola-stozkowe-przelozenie-c-196_56_58.html
Wychodzi zaledwie kilka setek różnicy miedzy modułem policzonym, a tym który można znaleźć w tabeli.
Tak jest, ale tylko gdy przełożenie będzie 1:1 zakładając, że osie kół są do siebie prostopadłe.RomanJ4 pisze: ponieważ zarys zęba jest pochylony pod kątem 45° do osi koła
Jeżeli będzie inne przełożenie i inna ilość zębów jednego i drugiego koła, to kąt o którym mówimy nie będzie równy 45°, tylko w jednym kole będzie np. 30° a w drugim 60°. I tu chociaż zdjęcia są słabe to nie powiedziałbym żeby miało 45°, tylko raczej mniej.
Kąt ten można sprawdzić z zależności:
σ=arc tg z1/z2
stąd widać że żeby kąt ten miał 45° ,to stosunek z1/z2 (czyli przełożenie) musiałby być równy 1. (tg45°=1)
A tom102 pisze że u niego przełożenie jest . 1/2. A w tym przypadku to mniejsze koło będzie miało 26,5° a drugie większe 63,5°
Ale to tak na marginesie, bo nawet przy innym kącie nie powinno być dużej różnicy między modułem obliczonym i najbliższym znormalizowanym posługując się tym w.w wzorem na moduł jak dla zwykłych kół walcowych.
Może koło mocno zużyte i pomiar średnicy niedokładny lub jakieś nietypowe koło robione w calu.














